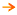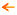
~When sampling with replacement, we consider the population size, N as infinite.
~When sampling without replacement and the sample size, n is greater
than 5% of the population size, N, we adjust the Margin of Error (which
in effect multiplies the standard deviation of the sample means) by the
Finite Population Correction factor: √[N-n)/(N-1)].
~This results in a slightly smaller margin of error, thus a slightly more
accurate result. Therefore, the confidence intervals constructed will be slightly narrower.
~Using the TI-83/84 for finding confidence intervals, we would multiply the entry for Sx (T-Interval) or sx (Z-Interval) by this quantity.
~Example: From a sample of 465 M&Ms (full bag), 100 are chosen randomly &
the weights are recorded. The mean weight was 0.8565 g with a
standard deviation of 0.0518 g. Construct a 95% confidence interval
estimate of the mean weight of M&Ms in the full bag from which the
sample was taken.
~Note: Since the sample size of 100 exceeds 5% of the population size
of 465 (number of M&Ms in the full bag), we use this correction.
TI-83/84 Procedure
1) Press Stat, Tests, menu 8 (TInterval), Enter
2) Press Stats, enter sample mean of 0.8565
3) Enter Sx: 0.0518 times 2nd √( (465-100)/464), Enter
Note: Many make mistakes in 3 due to the failure of using
parenthesis properly, so be careful here.
4) Enter n: 100
5) Enter C-Level: .95
6) Calculate, Enter
~The display shows the confidence interval (0.8474, 0.8656),
the sample mean, the adjusted standard deviation (slightly smaller),
followed by the sample size of 100.